
大图
大图
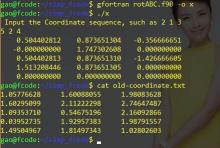
原始数据范例:
1.05776628 1.60088055 1.98083628
1.60295099 2.11222298 2.74647487
1.09353710 0.54675196 2.16092866
0.03952735 1.92957383 1.98791557
1.49504967 1.81497343 1.02802603
代码如下:
Module RotCoordMod ! 做成一个模块,可以直接插入到已有程序中
Implicit None
Integer , parameter :: DP = Selected_Real_Kind( p = 9 )
contains
Subroutine RotCoord( coord , coord1 , coord2 , coord3 )
!矩阵,要转换到原点的点、到Y正向的点、到XY平面的点
Real(kind=DP) :: coord(:,:)
Integer :: coord1,coord2,coord3
real(kind=DP) :: A(1,3),B(1,3),C(1,3),ab(1,3),ac(1,3),U(3,3),Ustar(3,3)
real(kind=DP) :: Lab(1,1),M(3,3),I(3,3)
A(1,:)=coord(:,coord1) ! 要转换到原点的点的坐标读入A
coord(1,:)=coord(1,:)-A(1,1)
coord(2,:)=coord(2,:)-A(1,2)
coord(3,:)=coord(3,:)-A(1,3) ! 这三步实现了整体坐标的平移,平移到了原点
A(1,:)=coord(:,coord1)
B(1,:)=coord(:,coord2)
C(1,:)=coord(:,coord3) ! 重新将要转换到原点的点、到Y正向的点、到XY平面的点的坐标读入A B C
ab=B-A !求A指向B的向量ab,其实此时就是B的坐标了。用ab表示,只是为了方便阅读
Lab=sqrt(matmul(ab,transpose(ab))) !利用矩阵乘积求ab的模Lab
ab(1,:)=[ab(1,1)/2, ((ab(1,2)+Lab(1,1))/2), ab(1,3)/2] !得到ab与Y轴正向的角平分线向量ab
Lab=sqrt(matmul(ab,transpose(ab))) !求新的ab的模
ab=ab/Lab(1,1) !将新的ab转换成单位长度的向量ab
U=matmul(transpose(ab),ab) !得到ab的方阵U
I=reshape((/1.0_DP ,0.0_DP ,0.0_DP ,0.0_DP ,1.0_DP ,0.0_DP ,0.0_DP ,0.0_DP ,1.0_DP/),(/3,3/)) !单位矩阵I
M=2*U- I
A=matmul(A,transpose(M))
B=matmul(B,transpose(M))
C=matmul(C,transpose(M)) ! ABC此时已经整体旋转至,AB平行于Y轴。这次旋转是180度的旋转
coord=transpose(matmul(transpose(coord),transpose(M))) ! 整体坐标已旋转至平行于Y轴
!接下来继续旋转ABC坐标,使C绕Y轴转至XY平面
ac=C-A ! 求A指向C的向量ac,其实此时就是c的坐标
ab(1,:)=[ 0.0_DP,1.0_DP,0.0_DP ] ! 直接构造Y轴方向的单位向量ab,之后,类似于上一次的旋转过程。
U=matmul(transpose(ab),ab) !得到ab的方阵U
Ustar=reshape((/0.0_DP,ab(1,3),-ab(1,2),-ab(1,3),0.0_DP,ab(1,1),ab(1,2),-ab(1,1),0.0_DP/),(/3,3/)) !U的共轭矩阵
M=U+ (I-U)*ac(1,1)/sqrt(ac(1,1)*ac(1,1)+ac(1,3)*ac(1,3))+ Ustar*ac(1,3)/sqrt(ac(1,1)*ac(1,1)+ac(1,3)*ac(1,3))
coord=transpose(matmul(transpose(coord),transpose(M))) ! 整体坐标已旋转完成
End Subroutine RotCoord
End Module RotCoordMod
Program www_fcode_cn
use RotCoordMod
Implicit None
integer :: i , j , k , io , coordmax = 0
Real(kind=DP) , allocatable :: coord(:,:) ! 声明可变二维数组coord
character(80) :: c
open(10,file='old-coordinate.txt',status="old")
Do ! 利用do循环确定坐标个数
read ( 10 ,'(A)',iostat=io) c
if (io < 0) exit
if (len_trim(c) == 0) cycle
coordmax = coordmax + 1
End Do
Rewind(10) ! 回到文件的开头
allocate( coord(3,coordmax) ) ! 配置可变二维数组coord
read( 10 , * ) coord(:,:) ! 将数据读入二维数组coord
write(*, * ) "Input the Coordinate sequence, such as 2 1 3"
read(*,*) i , j , k
call RotCoord( coord , i , j , k )
write( * , "(3f15.9)" ) coord(:,:) ! 屏幕显示变换结果
End Program www_fcode_cn
!我的方法笨了些,需要平移-->旋转-->再旋转。其实,这应该就是个正交变换,变换一次就够了,肯定有更便捷的已有的代码块。