设线性方程组 Ax=b 的系数矩阵 A 为 n 阶对称正定矩阵,用对称逐步超松弛迭代(SSOR法)的分裂矩阵作为预处理矩阵M,
M=\left ( 2-\omega \right )^{-1}\left ( D/\omega +L \right )\left ( D/\omega \right )^{-1}\left ( D/\omega +L \right )^{T}
式中:D 为 A 的对角阵;L 为 A 的严格下三角矩阵;0<\omega<2 为松弛因子。
SSOR-PCG法的迭代格式为:
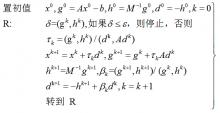
大图
林绍忠对其进行了改写,节省了一定的计算量,其具体算法为:令W=D/\omega+L,V=(2-\omega)D/\omega,y=W^{-1}g,Z=W^{T}d,则:
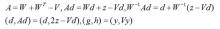
大图
于是,上述迭代公式可以改写为:
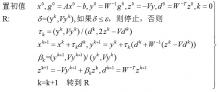
大图
代码及部分演示代码(请自行补充输入输出部分)如下:
Subroutine ssor_pcg_csr(nd, nnz, a, b, x, irw, jcol, eps, itmax, w, it, reg_err)
! ***********************************************************************************
! ** 本程序参考林绍忠《用预处理共轭梯度法求解有限元方程组及程序设计》改进的迭代格式
! ** 采用SSOR预处理,预处理矩阵为:M=(2-W)^{-1}*(D/W+L)*(D/W)^{-1}*(D/W+L)^{T}
! ** 在原来的程序基础上去掉ID映射的部分,而是一个小技巧来解决这个问题
! ** aliouying
! ** 2013-7-31
! ***********************************************************************************
Implicit None
! ***********************************************************************************
! ** 输入和输出
! ***********************************************************************************
Integer, Intent (In) :: nd, nnz
Integer, Intent (In) :: irw(nnz), jcol(nd+1) ! CSR压缩存储索引矩阵pointB,pointE
Complex (Kind=8), Intent (In) :: a(nnz), b(nd) ! 矩阵变量A*x=B
Complex (Kind=8), Intent (Inout) :: x(nd) ! 输入初始估计值和输出最终结果
Real (Kind=8), Intent (In) :: eps ! 收敛误差
Integer, Intent (In) :: itmax ! 最大迭代次数
Real (Kind=8), Intent (In) :: w ! 松弛因子
Integer, Intent (Out) :: it ! 收敛总计迭代次数
Real (Kind=8), Intent (Out) :: reg_err ! 迭代后的残差
! ***********************************************************************************
! ** 程序中间变量
! ***********************************************************************************
Complex (Kind=8) :: y(nd), z(nd), d(nd), v(nd), temp(nd)
Integer :: i
Complex (Kind=8) :: delta, tao, beta, delta1, delta0
Complex (Kind=8), External :: m_dot_product
! ***********************************************************************************
! ** 设置初始值
! ***********************************************************************************
Forall (i=1:nd)
v(i) = (2.0-w)*a(jcol(i))/w ! 这里V当成了一维向量,实际上它是一个对角矩阵,及A的对角阵计算来
! 若想节约内存,可以把用到V的地方用A(jcol())来代替,这里我主要是为
! 了程序跟理论公式的一致性
End Forall
! ***********************************************************************************
! ** 开始计算
! ***********************************************************************************
Call matmulvec_csr(nd, nnz, a, x, y, irw, jcol)
y = y - b
Call forward_solve(nd, nnz, a, y, y, irw, jcol, w)
Forall (i=1:nd) ! 这里可以直接用Z=V*Y代替,主要目的是为了方便替换V,而且forall的效率不错^_^
z(i) = -v(i)*y(i)
End Forall
Call back_solve(nd, nnz, a, z, d, irw, jcol, w)
it = 0
delta = m_dot_product(y, v*y, nd)
delta0 = delta
beta = 1
Do i = 1, itmax
! if( abs(delta) < EPS) then
! return
! endif
tao = delta/m_dot_product(d, 2.0*z-v*d, nd)
x = x + tao*d
! 多种收敛方式
! if( sqrt(sum(abs(tao*D/X)**2)) < EPS ) then
! return
! endif
Call forward_solve(nd, nnz, a, z-v*d, temp, irw, jcol, w)
y = y + tao*(temp+d)
delta1 = m_dot_product(y, v*y, nd)
beta = delta1/delta
z = -v*y + beta*z
Call back_solve(nd, nnz, a, z, d, irw, jcol, w)
delta = delta1
it = it + 1
reg_err = abs(delta/delta0)
! write(*,*) 'PCG iteration:',i,'of res:',reg_err
If (reg_err<eps) Then
Write (*, *) 'PCG iteration:', i, 'of res:', reg_err
Return
End If
End Do
Return
End Subroutine ssor_pcg_csr
! ================this is split line================================================!
Subroutine matmulvec_csr(nd, nnz, mat, vec, vec_out, irw, jcol)
Implicit None
! ***********************************************************************************
! ** 输入和输出
! ***********************************************************************************
Integer, Intent (In) :: nd, nnz
Integer, Intent (In) :: irw(nnz), jcol(nd+1) ! CSR压缩存储索引矩阵pointB,pointE
Complex (Kind=8), Intent (In) :: mat(nnz), vec(nd) ! 矩阵变量MAT和向量VEC
Complex (Kind=8) :: vec_out(nd) ! 输出最终结果
! ***********************************************************************************
! ** 程序中间变量
! ***********************************************************************************
Integer :: i, j
vec_out = (0.0D0, 0.0D0)
Do i = 1, nd
vec_out(i) = vec_out(i) + mat(jcol(i))*vec(i)
Do j = jcol(i) + 1, jcol(i+1) - 1
vec_out(i) = vec_out(i) + mat(j)*vec(irw(j))
vec_out(irw(j)) = vec_out(irw(j)) + mat(j)*vec(i)
End Do
End Do
Return
End Subroutine matmulvec_csr
! ================this is split line================================================!
Subroutine forward_solve(nd, nnz, mat, vec, vec_out, irw, jcol, w)
Implicit None
! ***********************************************************************************
! ** 输入和输出
! ***********************************************************************************
Integer, Intent (In) :: nd, nnz
Integer, Intent (In) :: irw(nnz), jcol(nd+1) ! CSR压缩存储索引矩阵pointB,pointE
Complex (Kind=8), Intent (In) :: mat(nnz), vec(nd) ! 矩阵变量MAT和向量VEC
Real (Kind=8), Intent (In) :: w
Complex (Kind=8), Intent (Out) :: vec_out(nd) ! 输出最终结果
! ***********************************************************************************
! ** 程序中间变量
! ***********************************************************************************
Integer :: i, j
vec_out = vec
Do i = 1, nd
vec_out(i) = vec_out(i)/mat(jcol(i))*w
Do j = jcol(i) + 1, jcol(i+1) - 1
vec_out(irw(j)) = vec_out(irw(j)) - mat(j)*vec_out(i)
End Do
End Do
Return
End Subroutine forward_solve
! ================this is split line================================================!
Subroutine back_solve(nd, nnz, mat, vec, vec_out, irw, jcol, w)
Implicit None
! ***********************************************************************************
! ** 输入和输出
! ***********************************************************************************
Integer, Intent (In) :: nd, nnz
Integer, Intent (In) :: irw(nnz), jcol(nd+1) ! CSR压缩存储索引矩阵pointB,pointE
Complex (Kind=8), Intent (In) :: mat(nnz), vec(nd) ! 矩阵变量MAT和向量VEC
Real (Kind=8), Intent (In) :: w
Complex (Kind=8), Intent (Out) :: vec_out(nd) ! 输出最终结果
! ***********************************************************************************
! ** 程序中间变量
! ***********************************************************************************
Integer :: i, j
Complex (Kind=8) :: sum
Do i = nd, 1, -1
sum = (0.0D0, 0.0D0)
Do j = jcol(i+1) - 1, jcol(i) + 1, -1
sum = sum + mat(j)*vec_out(irw(j))
End Do
vec_out(i) = (vec(i)-sum)/mat(jcol(i))*w
End Do
Return
End Subroutine back_solve
! ================this is split line================================================!
Function m_dot_product(a_in, b_in, n)
! ***********************************************************************************
! ** 向量的内积
! ***********************************************************************************
Implicit None
Integer :: n
Complex (Kind=8) :: a_in(n), b_in(n)
Complex (Kind=8) :: m_dot_product
Integer :: i
m_dot_product = 0.0
Do i = 1, n
m_dot_product = m_dot_product + a_in(i)*b_in(i)
End Do
Return
End Function m_dot_product
! ================this is split line================================================!
Subroutine id_change(nd, nnz, irw, jcol, icol, jrow, id_ch)
! ***********************************************************************************
! ** 矩阵A影射,由下三角CSC压缩存储影射到下三角CSR压缩存储
! ***********************************************************************************
Implicit None
! ***********************************************************************************
! ** 输入和输出
! ***********************************************************************************
Integer, Intent (In) :: nd, nnz
Integer, Intent (In) :: irw(nnz), jcol(nd+1) ! CSR压缩存储索引矩阵pointB,pointE
Integer, Intent (Out) :: icol(nnz), jrow(nd) ! CSC压缩存储索引矩阵pointB,pointE
Integer, Intent (Out) :: id_ch(nnz)
! ***********************************************************************************
! ** 程序中间变量
! ***********************************************************************************
Integer :: i, j, k, now_col_nnz, n
icol(1) = 1
jrow(1) = 1
now_col_nnz = 1
id_ch(1) = 1
n = 1
Do i = 2, nd
now_col_nnz = 0
Do j = 1, i - 1
Do k = jcol(j) + 1, jcol(j+1) - 1
If (irw(k)==i) Then
now_col_nnz = now_col_nnz + 1
n = n + 1
icol(n) = j
id_ch(n) = k
End If
End Do
End Do
now_col_nnz = now_col_nnz + 1
n = n + 1
icol(n) = i
id_ch(n) = jcol(i)
jrow(i) = jrow(i-1) + now_col_nnz
End Do
Return
End Subroutine id_change
! 下面是测试程序
Program www_fcode_cn
Implicit None
Complex (Kind=8) , allocatable :: x(:) , a(:) , rhs(:)
integer , allocatable :: jcol(:) , irw(:)
Real (Kind=8) :: w, eps, reg_err
Integer :: it , itmax , n , nnz
itmax = 1000
eps = 1.0D-20
w = 1
! 获得 n 和 nnz
Allocate (x(n),a(nnz),rhs(n),irw(nnz),jcol(n+1))
! 获得 a rhs
x = 0.0D0
! 调用程序
Call ssor_pcg_csr(n, nnz, a, rhs, x, irw ,jcol, eps, itmax, w, it, reg_err)
! 输出解
! write(*,*) X,IT,REG_ERR(IT)
Stop
End Program www_fcode_cn