Module Hankel_trans
Implicit None
Integer, Parameter :: Nn = 8 !设置kind的数值
Contains
!Fast Hankel Transform
!New digital linear filters for Hankel J0 and J1 transforms
!D Guptasarma, B Singh Geophysical prospecting, 1997
!f(r)=∫K(λ)Ji(rλ)dλ integral form
!Ji:Bessel function of the first kind and order i
!f(r)=(1/r)*∑{K(λi)*Wi} discrete form
!r:f(r)
!fun=K
!order:0 J0
!order:1 J1
Real (Kind=Nn) Function Hankel01(R, Fun, Order)
Implicit None
Real (Kind=Nn) R, Fun, F
Integer (Kind=4) Order
!-------------------------------------------------------------------------------
Real (Kind=Nn) J0_120(120), J1_140(140)
Real (Kind=Nn) A, S, Lambda(140)
!-------------------------------------------------------------------------------
Integer (Kind=4) I, N
!-------------------------------------------------------------------------------
Data J0_120/9.62801364263E-007_Nn, -5.02069203805E-006_Nn, 1.25268783953E-005_Nn, -1.99324417376E-005_Nn, 2.29149033546E-005_Nn, -2.04737583809E-005_Nn, 1.49952002937E-005_Nn, -9.37502840980E-006_Nn, 5.20156955323E-006_Nn, -2.62939890538E-006_Nn, 1.26550848081E-006_Nn, -5.73156151923E-007_Nn, 2.76281274155E-007_Nn, -1.09963734387E-007_Nn, 7.38038330280E-008_Nn, -9.31614600001E-009_Nn, 3.87247135578E-008_Nn, 2.10303178461E-008_Nn, 4.10556513877E-008_Nn, 4.13077946246E-008_Nn, 5.68828741789E-008_Nn, 6.59543638130E-008_Nn, 8.40811858728E-008_Nn, 1.01532550003E-007_Nn, 1.26437360082E-007_Nn, 1.54733678097E-007_Nn, 1.91218582499E-007_Nn, 2.35008851918E-007_Nn, 2.89750329490E-007_Nn, 3.56550504341E-007_Nn, 4.39299297826E-007_Nn, 5.40794544880E-007_Nn, 6.66136379541E-007_Nn, 8.20175040653E-007_Nn, 1.01015545059E-006_Nn, 1.24384500153E-006_Nn, 1.53187399787E-006_Nn, 1.88633707689E-006_Nn, 2.32307100992E-006_Nn, 2.86067883258E-006_Nn, 3.52293208580E-006_Nn, 4.33827546442E-006_Nn, 5.34253613351E-006_Nn, &
6.57906223200E-006_Nn, 8.10198829111E-006_Nn, 9.97723263578E-006_Nn, 1.22867312381E-005_Nn, 1.51305855976E-005_Nn, 1.86329431672E-005_Nn, 2.29456891669E-005_Nn, 2.82570465155E-005_Nn, 3.47973610445E-005_Nn, 4.28521099371E-005_Nn, 5.27705217882E-005_Nn, 6.49856943660E-005_Nn, 8.00269662180E-005_Nn, 9.85515408752E-005_Nn, 1.21361571831E-004_Nn, 1.49454562334E-004_Nn, 1.84045784500E-004_Nn, 2.26649641428E-004_Nn, 2.79106748890E-004_Nn, 3.43716968725E-004_Nn, 4.23267056591E-004_Nn, 5.21251001943E-004_Nn, 6.41886194381E-004_Nn, 7.90483105615E-004_Nn, 9.73420647376E-004_Nn, 1.19877439042E-003_Nn, 1.47618560844E-003_Nn, 1.81794224454E-003_Nn, 2.23860214971E-003_Nn, 2.75687537633E-003_Nn, 3.39471308297E-003_Nn, 4.18062141752E-003_Nn, 5.14762977308E-003_Nn, 6.33918155348E-003_Nn, 7.80480111772E-003_Nn, 9.61064602702E-003_Nn, 1.18304971234E-002_Nn, 1.45647517743E-002_Nn, 1.79219149417E-002_Nn, 2.20527911163E-002_Nn, 2.71124775541E-002_Nn, 3.33214363101E-002_Nn, 4.08864842127E-002_Nn, 5.01074356716E-002_Nn, &
6.12084049407E-002_Nn, 7.45146949048E-002_Nn, 9.00780900611E-002_Nn, 1.07940155413E-001_Nn, 1.27267746478E-001_Nn, 1.46676027814E-001_Nn, 1.62254276550E-001_Nn, 1.68045766353E-001_Nn, 1.52383204788E-001_Nn, 1.01214136498E-001_Nn, -2.44389126667E-003_Nn, -1.54078468398E-001_Nn, -3.03214415655E-001_Nn, -2.97674373379E-001_Nn, 7.93541259524E-003_Nn, 4.26273267393E-001_Nn, 1.00032384844E-001_Nn, -4.94117404043E-001_Nn, 3.92604878741E-001_Nn, -1.90111691178E-001_Nn, 7.43654896362E-002_Nn, -2.78508428343E-002_Nn, 1.09992061155E-002_Nn, -4.69798719697E-003_Nn, 2.12587632706E-003_Nn, -9.81986734159E-004_Nn, 4.44992546836E-004_Nn, -1.89983519162E-004_Nn, 7.31024164292E-005_Nn, -2.40057837293E-005_Nn, 6.23096824846E-006_Nn, -1.12363896552E-006_Nn, 1.04470606055E-007_Nn/
Data J1_140/ -6.76671159511E-014_Nn, 3.39808396836E-013_Nn, -7.43411889153E-013_Nn, 8.93613024469E-013_Nn, -5.47341591896E-013_Nn, -5.84920181906E-014_Nn, 5.20780672883E-013_Nn, -6.92656254606E-013_Nn, 6.88908045074E-013_Nn, -6.39910528298E-013_Nn, 5.82098912530E-013_Nn, -4.84912700478E-013_Nn, 3.54684337858E-013_Nn, -2.10855291368E-013_Nn, 1.00452749275E-013_Nn, 5.58449957721E-015_Nn, -5.67206735175E-014_Nn, 1.09107856853E-013_Nn, -6.04067500756E-014_Nn, 8.84512134731E-014_Nn, 2.22321981827E-014_Nn, 8.38072239207E-014_Nn, 1.23647835900E-013_Nn, 1.44351787234E-013_Nn, 2.94276480713E-013_Nn, 3.39965995918E-013_Nn, 6.17024672340E-013_Nn, 8.25310217692E-013_Nn, 1.32560792613E-012_Nn, 1.90949961267E-012_Nn, 2.93458179767E-012_Nn, 4.33454210095E-012_Nn, 6.55863288798E-012_Nn, 9.78324910827E-012_Nn, 1.47126365223E-011_Nn, 2.20240108708E-011_Nn, 3.30577485691E-011_Nn, 4.95377381480E-011_Nn, 7.43047574433E-011_Nn, 1.11400535181E-010_Nn, 1.67052734516E-010_Nn, 2.50470107577E-010_Nn, 3.75597211630E-010_Nn, &
5.63165204681E-010_Nn, 8.44458166896E-010_Nn, 1.26621795331E-009_Nn, 1.89866561359E-009_Nn, 2.84693620927E-009_Nn, 4.26886170263E-009_Nn, 6.40104325574E-009_Nn, 9.59798498616E-009_Nn, 1.43918931885E-008_Nn, 2.15798696769E-008_Nn, 3.23584600810E-008_Nn, 4.85195105813E-008_Nn, 7.27538583183E-008_Nn, 1.09090191748E-007_Nn, 1.63577866557E-007_Nn, 2.45275193920E-007_Nn, 3.67784458730E-007_Nn, 5.51470341585E-007_Nn, 8.26916206192E-007_Nn, 1.23991037294E-006_Nn, 1.85921554669E-006_Nn, 2.78777669034E-006_Nn, 4.18019870272E-006_Nn, 6.26794044911E-006_Nn, 9.39858833064E-006_Nn, 1.40925408889E-005_Nn, 2.11312291505E-005_Nn, 3.16846342900E-005_Nn, 4.75093313246E-005_Nn, 7.12354794719E-005_Nn, 1.06810848460E-004_Nn, 1.60146590551E-004_Nn, 2.40110903628E-004_Nn, 3.59981158972E-004_Nn, 5.39658308918E-004_Nn, 8.08925141201E-004_Nn, 1.21234066243E-003_Nn, 1.81650387595E-003_Nn, 2.72068483151E-003_Nn, 4.07274689463E-003_Nn, 6.09135552241E-003_Nn, 9.09940027636E-003_Nn, 1.35660714813E-002_Nn, 2.01692550906E-002_Nn, &
2.98534800308E-002_Nn, 4.39060697220E-002_Nn, 6.39211368217E-002_Nn, 9.16763946228E-002_Nn, 1.28368795114E-001_Nn, 1.73241920046E-001_Nn, 2.19830379079E-001_Nn, 2.51193131178E-001_Nn, 2.32380049895E-001_Nn, 1.17121080205E-001_Nn, -1.17252913088E-001_Nn, -3.52148528535E-001_Nn, -2.71162871370E-001_Nn, 2.91134747110E-001_Nn, 3.17192840623E-001_Nn, -4.93075681595E-001_Nn, 3.11223091821E-001_Nn, -1.36044122543E-001_Nn, 5.12141261934E-002_Nn, -1.90806300761E-002_Nn, 7.57044398633E-003_Nn, -3.25432753751E-003_Nn, 1.49774676371E-003_Nn, -7.24569558272E-004_Nn, 3.62792644965E-004_Nn, -1.85907973641E-004_Nn, 9.67201396593E-005_Nn, -5.07744171678E-005_Nn, 2.67510121456E-005_Nn, -1.40667136728E-005_Nn, 7.33363699547E-006_Nn, -3.75638767050E-006_Nn, 1.86344211280E-006_Nn, -8.71623576811E-007_Nn, 3.61028200288E-007_Nn, -1.05847108097E-007_Nn, -1.51569361490E-008_Nn, 6.67633241420E-008_Nn, -8.33741579804E-008_Nn, 8.31065906136E-008_Nn, -7.53457009758E-008_Nn, 6.48057680299E-008_Nn, -5.37558016587E-008_Nn, &
4.32436265303E-008_Nn, -3.37262648712E-008_Nn, 2.53558687098E-008_Nn, -1.81287021528E-008_Nn, 1.20228328586E-008_Nn, -7.10898040664E-009_Nn, 3.53667004588E-009_Nn, -1.36030600198E-009_Nn, 3.52544249042E-010_Nn, -4.53719284366E-011_Nn/
!-------------------------------------------------------------------------------
Select Case (Order)
Case (0) !J0
A = -8.38850000000D0
S = 9.04226468670D-2
N = 120
Do I = 1, N
Lambda(I) = ((10.0D0+0_Nn)**(A+Real(I-1,Nn)*S))/R
End Do
F = 0.0D0+0_Nn
Do I = 1, N
F = F + Fun(Lambda(I))*J0_120(I)
End Do
Hankel01 = F/R
Case (1) !J1
A = -7.91001919000D0
S = 8.79671439570D-2
N = 140
Do I = 1, N
Lambda(I) = ((10.0D0+0_Nn)**(A+Real(I-1,Nn)*S))/R
End Do
F = 0.0D0+0_Nn
Do I = 1, N
F = F + Fun(Lambda(I))*J1_140(I)
End Do
Hankel01 = F/R
Case Default
Write (*, '(a)') 'Hankel transform ERROR!order should be 0 or 1'
End Select
End Function Hankel01
Real (Kind=Nn) Function Hankel_check(B) !核函数 K
Implicit None
Real (Kind=Nn) B
Hankel_check = B*Exp(-B)
End Function Hankel_check
End Module Hankel_trans
!测试主程序
Program www_fcode_cn
Use Hankel_trans
Implicit None
Integer i
Do i = 1, 400
Write (*, *) Hankel01( i*1.0_nn , Hankel_check , 1 )
End Do
End Program www_fcode_cn
测试J1,误差如下图: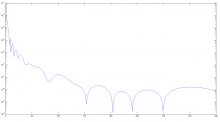
大图