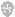高斯勒让德求积分Fortran程序——自带求任意阶高斯点及相应权重的程序
句号大师（王培杰）编写，岸边的鱼（小超超小鱼）整理，标注
最近，因为要求解一些剧烈变化（且积分区间跨度比较大）的函数积分问题，想到了高斯型求积分公式，随查阅各种算法书籍，但无奈算法书上给出的都是利用五阶高斯勒让德公式求解积分的程序。经石子儿兄弟指点，认识到五阶高斯勒让德公式求解精度实在是有点小低，（解决办法有两个，一是本文的增加高斯结点，而是采用变步长高斯求积分法，此法将另文讨论。）石子儿兄弟建议将精度至少提高到300—500之间，那将面对自己计算高斯点及权系数的问题。无奈之下，遍寻各大编程网站，终于在我们亲爱的fcode.cn网站上找到了句号大师的一篇帖子，随私聊句号大师,感谢慷慨的句号大师将修改好的程序无私的传给我，感动之余，觉得有必要将这一成果整理，标注后发回我们的网站上供广大网友下载使用。
声明：下文程序整体由句号大师（王培杰）传递给我，仅对其表示由衷的感谢。我负责添加标注，设置了两个输出到文件的功能。另，句号大师提醒广大网友，高斯型求积公式不是高斯点越多越精确，高斯点变多后会有很多的截断误差。
001 | Module gsld !高斯—勒让德积分高斯点及权重的求解模块 |
002 | Implicit None |
003 | Integer, Parameter :: n = 5 !设置求解高斯点的个数 |
004 | Integer, Parameter :: DP = Selected_Real_Kind( p=13 ) !设置kind的数值 |
005 | Real(kind=DP) , parameter :: EPS = 1.0e-15_DP !精度设置 |
006 |
007 | Contains |
008 |
009 | Real(Kind=DP) Function f(x) !定义函数f（x） |
010 | Implicit None |
011 | Integer :: i |
012 | Real (Kind=DP) :: a(n), x !a(n)代表n阶勒让德多项式 |
013 | a(1) = x !1阶勒让德多项式 |
014 | a(2) = 1.5_DP*(x**2) - 0.5_DP !2阶勒让德多项式 |
015 | Do i = 3, n |
016 | a(i) = (2*i-1)*x*a(i-1)/i - (i-1)*a(i-2)/i |
017 | !利用递推关系产生n阶勒让德多项式 |
018 | End Do |
019 | f = a(n) !生成的n阶勒让德多项式 |
020 | End Function f |
021 |
022 | Real(Kind=DP) Function f1(x) |
023 | Implicit None |
024 | Integer :: i |
025 | Real (Kind=DP) :: a(n), x |
026 | a(1) = x |
027 | a(2) = 1.5_DP*x**2 - 0.5_DP |
028 | Do i = 3, n - 1 |
029 | a(i) = (2*i-1)*x*a(i-1)/i - (i-1)*a(i-2)/i |
030 | End Do |
031 | f1 = a(n-1) !生成的（n-1）阶勒让德多项式 |
032 | End Function f1 |
033 |
034 | Real (Kind=DP) Function g(x) |
035 | Implicit None |
036 | Integer :: i |
037 | Real (Kind=DP) :: a(n), x |
038 | a(1) = x |
039 | a(2) = 1.5_DP*x**2 - 0.5_DP |
040 | Do i = 3, n |
041 | a(i) = (2*i-1)*x*a(i-1)/i - (i-1)*a(i-2)/i |
042 | End Do |
043 | g = n*a(n-1)/(1-x**2) - n*x*a(n)/(1-x**2) |
044 | !生成n阶勒让德多项式的导数表达式 |
045 | End Function g |
046 |
047 | Real (Kind=DP) Function bis(a, b) !二分法求解函数的解 |
048 | Implicit None |
049 | Real (Kind=DP) :: a, b, c |
050 | !a,b是传递进来的划分好的有一个解存在的区间 |
051 | Do |
052 | c = (a+b)/2.0_DP |
053 | If (f(c)*f(a)<0) Then |
054 | b = c |
055 | Else |
056 | a = c |
057 | End If |
058 | If ((b-a)<EPS) exit |
059 | End Do |
060 | bis = c!bis即是利用二分法求得的解 |
061 | End Function bis |
062 |
063 | Subroutine fn0(fn, ak) |
064 | Implicit None |
065 | Real (Kind=DP) :: m, fn(n), ak(n) |
066 | !定义数组,大小n由module开始声明。 |
067 | Integer :: i, j |
068 | j = 0 !赋值控制循环变量的初值 |
069 | m = -1.000001 !设置计算域[-1，1] 的下限，即代替-1 |
070 | Do i = 1, 200000 !这个循环次数应该是由步长0.00001决 定,计算方法：200000=2/0.000001 |
071 | If (f(m)*f(m+0.00001)<0) Then !从下限处开始往上逐步累加， |
072 | !由步长0.00001说明最多求解10^5个解 |
073 | j = j + 1 !记录这是第几个解 |
074 | fn(j) = bis(m, m+0.00001) |
075 | !调用二分法求解程序在分好的一小段上求解， |
076 | !将解存储在fn（j） |
077 | ak(j) = 2.0_DP/(n*f1(fn(j))*g(fn(j))) !高斯点的权重 |
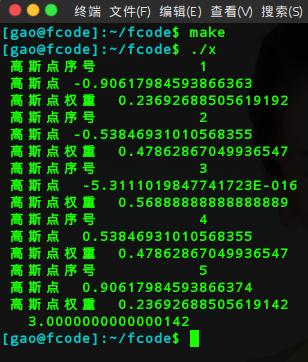
078 | Write (*, *) '高斯点序号', j |
079 | Write (*, *) '高斯点', fn(j) |
080 | Write (*, *) '高斯点权重', ak(j) |
081 | End If |
082 | m = m + 0.00001 !执行完一次判断m向前推进一步 |
083 | End Do |
084 | End Subroutine fn0 |
085 |
086 | End Module gsld |
087 |
088 | Program www_fcode_cn |
089 | Use gsld |
090 | Implicit None |
091 | Real (Kind=DP) :: fn(n), ak(n), x, a, b, answer |
092 | Integer :: i |
093 | Call fn0(fn, ak) !调用求高斯零点和权重的子函数 |
094 | a = 0.0_DP !积分上限 |
095 | b = 1.0_DP !积分下限 |
096 | answer = 0.0_DP !求积分结果赋初始值 |
097 | Do i = 1, n |
098 | answer = answer + ak(i)*y((a+b)/2.0_DP+(b-a)/2.0_DP*fn(i)) |
099 | !部分高斯勒让德求积分公式 |
100 | End Do |
101 | answer = answer*(b-a)/2.0_DP |
102 | Write (*, *) '高斯_勒让德求积分结果', answer |
103 |
104 | contains |
105 |
106 | Real (Kind=DP) Function y(x) !被积函数 |
107 | Implicit None |
108 | Real (Kind=DP) :: x |
109 | y = x**2/3.0_DP !每次计算在这里修改被积函数即可 |
110 | End Function y |
111 |
112 | End Program www_fcode_cn |
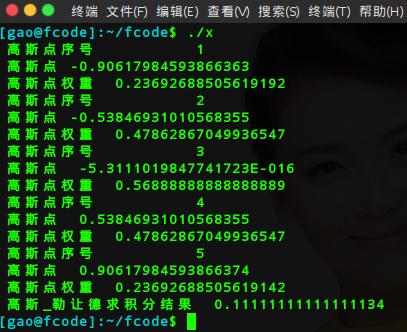
以下是使用高斯勒让德函数计算三重积分的例子：
01 | Program www_fcode_cn |
02 | Use gsld |
03 | Implicit None |
04 | Real(kind=DP) :: fn(n), ak(n), x, x1, x2, a, b, a1, b1, a2, b2, answer |
05 | Integer :: i, j, k |
06 | Call fn0(fn, ak) |
07 | a = 0 |
08 | b = 1 !积分上下限 |
09 | a1 = 0 |
10 | b1 = 1 |
11 | a2 = 0 |
12 | b2 = 1 |
13 | answer = 0 |
14 | Do k = 1, n |
15 | Do j = 1, n |
16 | Do i = 1, n |
17 | answer = answer + ak(i)*ak(j)*ak(k)*y((a+b)/2+(b-a)/2*fn(i), (a1+b1)/2+(b1-a1)/2*fn(j), (a1+b1)/2+(b1-a1)/2*fn(k)) |
18 | End Do |
19 | End Do |
20 | End Do |
21 | answer = answer*(b-a)/2*(b1-a1)/2*(b2-a2)/2 |
22 | Write (*, *) answer |
23 |
24 | contains |
25 | |
26 | Real(kind=DP) Function y(x, x1, x2) !被积函数 |
27 | Real(kind=DP) :: x, x1, x2 |
28 | y = 2*x + 2*x1 + 2*x2 |
29 | End Function y |
30 |
31 | End Program www_fcode_cn |
